1.5. Example: Solving inviscid Burgers’ equation from Python using IVP interface

Here we demonstrate how to use the ivp (initial-value problem for ordinary differential equations, that is, time integration) interface with Python bindings to solve the following problem based on the inviscid Burgers’ equation:

\[\begin{split} \begin{align} u_t + \left(\frac{u^2}{2}\right)_x &= 0, \quad x \in [0, 2], \quad t \in [0, 2], \\ u(0, x) &= 0.5 - 0.25 \sin(\pi x), \\ u(t, 0) &= u(t, 2) \end{align} \end{split}\]

This is one of the most famous nonlinear hyperbolic equations with the property that some initial conditions, although smooth, can lead to jump discontinuities in the solution at some final time. These jump discontinuities are called shock waves. The initial condition that we choose is exactly of this type, so that at the final time \(T = 2\) the solution develops a shock wave.

To deal with such properties, special numerical methods are used that smooth the discontinuity a bit so that the computation process remains stable.

Also, it is common to use special time integration schemes with an upper bound on the time step, also to keep things numerically stable.

Here, instead of using such special methods for time integration, we will use adaptive integration. To facilitate this, we will convert the partial differential equation into a system of ODEs:

\[ \frac{du_i}{dt} = -\frac12 \frac{\partial u_i^2}{\partial x}, \quad i = 0, \dots, N, \]

which is the discretization on the grid with resolution \(N\) and spatial step \(\Delta x = 2 / N\). Further, the partial derivative on the right-hand side is approximated as

(1.5.1)\[\frac{du_i}{dt} = - \frac{\hat f(u_{i + 1/2}) - \hat f(u_{i - 1/2})}{\Delta x},\]

where \(f = 0.5 u^2\) and \(\hat f\) is an approximation of \(f\). There are different ways of approximating \(f\), we will use one of the simplest (called global Lax–Friedrichs flux) just for the sake of demonstration:

(1.5.2)\[\hat f = \frac{f_i + f_{i+1}}{2} - \frac{c (u_{i+1} - u_i)}{2},\]

where \(c = \max u_i\), \(i = 1, \dots, N\).

We start with necessary imports:

import matplotlib.pyplot as plt
import numpy as np
from openinterfaces.interfaces.ivp import IVP

where the last import is the IVP gateway component that provides a common interface to different implementations of time integrators.

Next, we define an auxiliary class BurgersEquationProblem that computes an initial conditions for the given grid resolution \(N\), defines the time span of the problem, and provides the right-hand side of the system as a method compute_rhs:

class BurgersEquationProblem:
    def __init__(self, N=101):
        self.N = N

        self.x, self.dx = np.linspace(0, 2, num=N, retstep=True)
        self.u = 0.5 - 0.25 * np.sin(np.pi * self.x)
        self.invariant = np.sum(np.abs(self.u))

        self.cfl = 0.5
        self.dt_max = self.dx * self.cfl

        self.t0 = 0.0
        self.tfinal = 2.0

    def compute_rhs(self, t, u, udot, user_data):
        dx = self.dx

        f = 0.5 * u**2
        local_ss = np.maximum(np.abs(u[0:-1]), np.abs(u[1:]))
        local_ss = np.max(np.abs(u))
        f_hat = 0.5 * (f[0:-1] + f[1:]) - 0.5 * local_ss * (u[1:] - u[0:-1])
        f_plus = f_hat[1:]
        f_minus = f_hat[0:-1]
        udot[1:-1] = -1.0 / dx * (f_plus - f_minus)

        local_ss_rb = np.maximum(np.abs(u[0]), np.abs(u[-1]))
        f_rb = 0.5 * (f[0] + f[-1]) - 0.5 * local_ss_rb * (u[0] - u[-1])
        f_lb = f_rb

        udot[+0] = -1.0 / dx * (f_minus[0] - f_lb)
        udot[-1] = -1.0 / dx * (f_rb - f_plus[-1])

Note that the method compute_rhs has a signature rhs(t, u, udot, user_data), defined by the IVP interface, where t and u are the current time and the solution vector, respectively, udot is the vector where the computed right-hand side is written, and user_data is an optional argument that can be used to pass additional data to the function. Here, we ignore this argument because the user data (spatial step dx) is already stored as a member variable of the class. Also, note that the right-hand side function returns 0 to indicate success.

Because this problem is of the hyperbolic type, we can use the Dormand–Prince method provided via the scipy_ode implementation:

impl = "scipy_ode_dopri5"
s = IVP(impl)

and then instantiate the auxiliary problem class and pass the details of the problem to the IVP instance:

problem = BurgersEquationProblem(N=101)
s.set_initial_value(problem.u0, problem.t0)
s.set_rhs_fn(problem.compute_rhs)

particularly, we set the initial condition using the method set_initial_value and the right-hand side function using the method set_rhs_fn. Invoking these two methods is enough to fully define the problem as we keep the default tolerances and other parameters of the integrator.

Then we define the time points at which we want to compute the solution:

    times = np.linspace(problem.t0, problem.tfinal, num=11)

and finally do the actual time integration, acculumating the solution at the specified time points:

    soln = [problem.u0]
    for t in times[1:]:
        s.integrate(t)
        soln.append(s.y)

After the integration is done, we can plot the results:

    plt.plot(problem.x, soln[0], "--", label="Initial condition")
    plt.plot(problem.x, soln[-1], "-", label="Final solution")
    plt.xlabel(r"$x$")
    plt.ylabel(r"Solution of Burgers' equation")
    plt.legend(loc="best")
    plt.tight_layout(pad=0.1)
    plt.show()

The actual solution at the final time \(T = 2\) and the initial condition are shown on the figure Fig. 1.5.1.

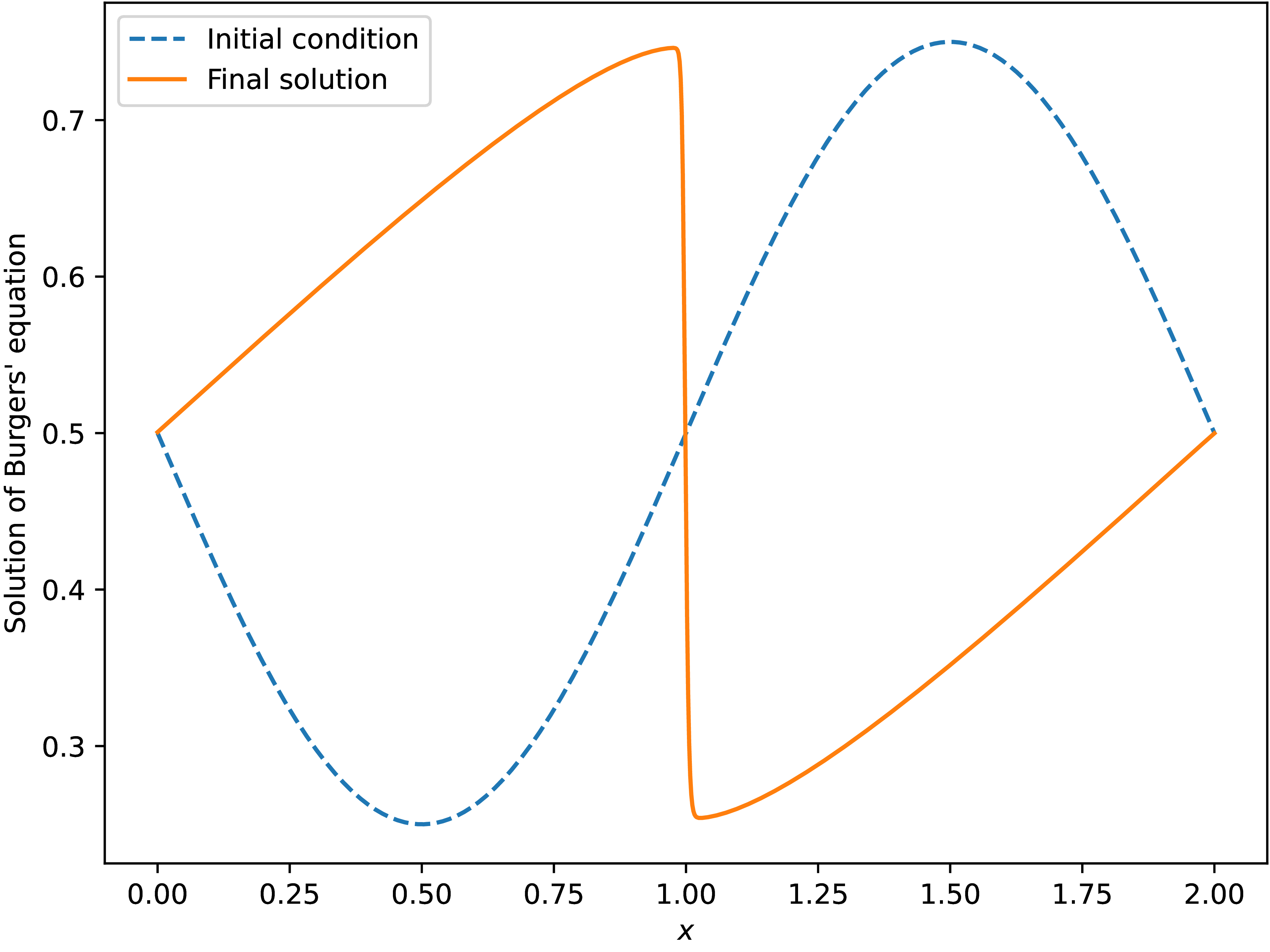
Fig. 1.5.1 Numerical solution of the problem for Burgers’ equation via IVP interface of Open Interfaces using scipy_ode implementation.

The complete code is available in the repository, is compiled during building the source code and after building can be run as:

python examples/call_ivp_from_python_burgers_eq.py [implementation]

where [implementation] is the name of the implementation to use, one of the following:

• scipy_ode (SciPy ODE solvers in Python),

• sundials_cvode (SUNDIALS CVODE solver in C),

• jl_diffeq (OrdinaryDiffEq.jl solvers in Julia).